Symmetry, generally speaking, a balance or correspondence between various parts of an object; the term symmetry is used both in the arts and in the sciences. In art and design, it is often used in a somewhat loose sense, to mean a kind of balance in which the corresponding parts are not necessarily alike but only similar. A symmetrical design should produce a pleasing effect; if there is too close a correspondence, the effect may be monotonous. Ancient Greek architecture is particularly distinguished for its symmetry. In modern art, the Dutch artist M. Escher achieved a number of striking effects in his works exploring mathematical symmetry.

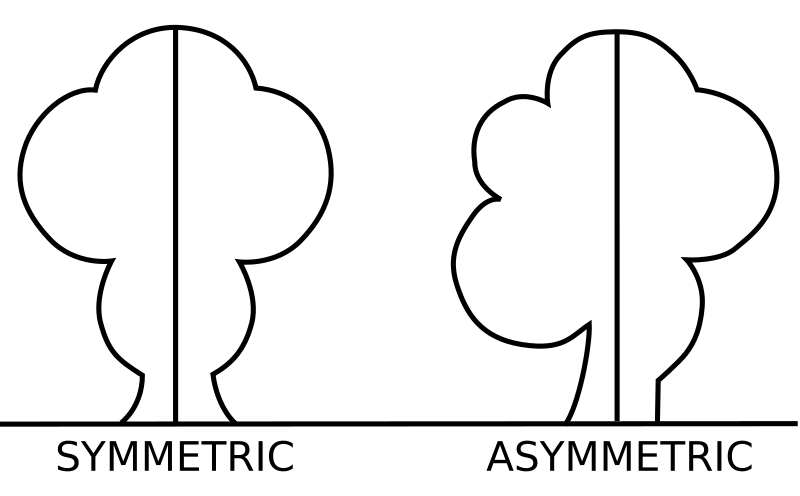
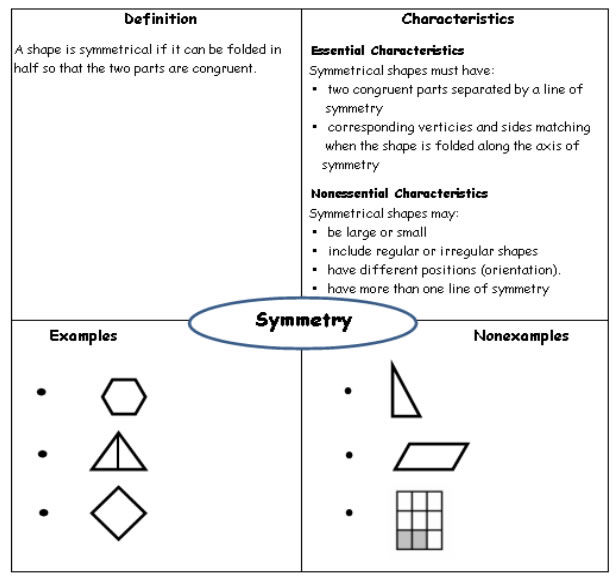
Symmetry meaning, definition, what is symmetry: the quality of being symmetrical: Learn more. Symmetry is when a shape looks identical to its original shape after being flipped or turned. Symmetry is thus a mirror image. Symmetry exists everywhere in our life.

A mathematical operation, or transformation, that results in the same figure as the original figure (or its mirror image) is called a symmetry operation. Such operations include reflection, rotation, double reflection, and translation.

The set of all operations on a given figure that leave the figure unchanged constitutes the symmetry group,in mathematics, system consisting of a set of elements and a binary operation a+ b defined for combining two elements such that the following requirements are satisfied: (1) The set is closed under the operation; i.e. Click the link for more information. for that figure.

The symmetry groups of three-dimensional figures are of special interest because of their application in fields such as crystallography (see crystal,a solid body bounded by natural plane faces that are the external expression of a regular internal arrangement of constituent atoms, molecules, or ions. The formation of a crystal by a substance passing from a gas or liquid to a solid state, or going out of solution (by. Click the link for more information.). In general, a symmetry operation on a figure is defined with respect to a given point (center of symmetry), line (axis of symmetry), or plane (plane of symmetry).

In biology, symmetry is studied in the correspondences between different parts of a given organism, as between the left and right halves of the human body or between the various segments of a starfish (see symmetry, biological,similarity or balance between parts of an organism so that when a straight cut is made through a point or along a line, equal, mirror-image halves are formed. Symmetry in body shapes is related to the lifestyles of organisms.

Click the link for more information.). In physics, basic symmetries in nature underlie the various conservation laws,in physics, basic laws that together determine which processes can or cannot occur in nature; each law maintains that the total value of the quantity governed by that law, e.g., mass or energy, remains unchanged during physical processes. Click the link for more information. For example, the symmetry of space and time with respect to translation and rotation means that a given experiment should yield the same results regardless of where it is performed, what direction the equipment is pointing in, or when it is performed.

These three symmetries can be shown to imply the laws of conservation of linear momentum, angular momentum, and energy, respectively. BibliographySee G. Martin, Transformation Geometry (1987); B. Bunch, Reality's Mirror (1989); M. Escher, Escher on Escher (tr. REFERENCESGauze, G.

Asimmetriia protoplazmy. Moscow-Leningrad, 1940.Vainshtein, B. Difraktsiia rentgenovykh luchei na tsepnykh molekulakh. Moscow, 1963.Beklemishev, V. Osnovy sravnitel’noi analomii bespozvonochnykh, 3rd ed., vols. Moscow, 1964.Urmantsev, Iu. Simmetriia prirody i priroda simmetrii.

Moscow, 1974.Ludwig, W. Das Rechts-Links-Problem im Tierrich und beim Menschen.

Berlin-Heidelberg-New York, 1970.Bentley, R. Molecular Asymmetry in Biology, vols. New York, 1969–70. Plane figure symmetric with respect to the line AB; reflection in AB carries the point M to M″A reflection is an example of an orthogonal transformation that, in contrast to a direct motion, changes orientation. Any orthogonal transformation can be carried out by successively performing a finite number of reflections; this fact plays an important role in the investigation of the symmetry of geometric figures.(2) Symmetry, in the broad sense, is the property of a geometric figure Φ that characterizes some regularity of the shape of Φ, or the invariance of Φ under motions. More precisely, Φ has symmetry, or is symmetric, if there exists a nontrivial orthogonal transformation that maps Φ onto itself.

The set of all orthogonal transformations that map Φ onto itself is called the symmetry group of Φ; the transformations are themselves sometimes called symmetries.Thus, if a plane figure is mapped onto itself under reflection, it is symmetric with respect to a line, which is the axis of symmetry (Figure 1). The symmetry group in this case consists of two elements. Suppose the plane figure Φ is such that rotations with respect to some point O through an angle of 360°/ n, where n is an integer ≥ 2, map Φ onto itself; Φ is then said to have n-fold symmetry with respect to O, which is called the center of symmetry. Regular polygons (Figure 2) are examples of such figures; here, the symmetry group is a cyclic group of order n. A circle has infinite-fold symmetry, since it is mapped onto itself by rotation through any angle.In addition to the symmetry produced by reflections, the simplest types of spatial symmetry include central symmetry, axial symmetry, and translational symmetry.In the case of central symmetry (central inversion) or reflection in a point O, a figure Φ is mapped onto itself by successive reflections in three mutually perpendicular planes.

Use your words game mac. Use Your Words is a digital party game for funny people and their unfunny friends! Coming soon to Steam, Xbox One, PlayStation 4 and Apple TV!

In other words, O is the midpoint of the line segment joining symmetric points of Φ (Figure 3). Star-shaped regular polygon possessing eightfold symmetry with respect to its centerIn the case of axial symmetry, or n-fold symmetry with respect to a line, a figure is mapped onto itself by rotation about some straight line, the axis of symmetry, through an angle of 360°/ n. For example, the line AB is an axis of threefold symmetry, or threefold axis, of the cube, and the line CD is an axis of fourfold symmetry, or fourfold axis (Figure 3). In general, regular and semiregular polyhedrons are symmetric with respect to a number of lines. The location, number, and multiplicity of the axes of symmetry play an important role in crystallography.A figure is said to have rotatory reflection symmetry if it can be mapped onto itself by a combination of a rotation through an angle of 360°/2 k about a line AB and a reflection in a plane perpendicular to that line. A B is a 2k-fold rotoflection axis and a k-fold axis of symmetry (Figure 4).

A twofold rotatory reflection is equivalent to a central inversion.In the case of translational symmetry, the figure is mapped onto itself by translation along some line, the axis of translation. For example, a figure with a single translation axis has an infinite set of planes of symmetry, since any translation can be carried out by two successive reflections in planes perpendicular to the axis of translation (Figure 5). Figures that have several axes of translation play an important role in the investigation of crystal lattices.

Cube: ( AB) a threefold axis of symmetry, (CD) a fourfold axis, (O) center of symmetry; the points M and M’ are symmetric with respect to AB, CD, and OIn art, symmetry is a widely used device for making a composition harmonious. Works of decorative applied art exhibit symmetry, as do works of architecture. Symmetry is an indispensable quality of a structure as a whole or at least of its parts and details—for example, of its plan, facade, columns, and capitals. Symmetry is also the basic device for making borders and ornament, which are plane figures that have, respectively, one or several translational symmetries combined with reflections.Reflections and rotations can be used to generate all symmetries of figures. Combinations of symmetries generated by reflections, rotations, and translations are the subject of investigation in various fields of natural science. For example, a twist, which involves rotation through some angle about an axis followed by a translation along the axis, has a botanical application in phyllotaxy (literally, “leaf arrangement”).

The symmetry of a molecular configuration affects the physical and chemical characteristics of the molecules and is of importance in the theoretical analysis of the structure of compounds, the properties of compounds, and the behavior of compounds in various reactions. The role of the geometric symmetry of crystals and lattices in the physical sciences has already been mentioned; in addition, concepts of symmetry in a more general sense are of great importance. Thus, the symmetry of space-time, as expressed in its homogeneity and isotropy ( see RELATIVITY, THEORY OF), makes possible the establishment of the conservation laws. Generalized symmetry plays an important role in the formation of atomic spectra and in the classification of elementary particles. Polyhedron possessing rotatory reflection symmetry: ( AB) fourfold rotoflection axis(3) Symmetry, in the general sense, means the invariance of the structure of a mathematical or physical object with respect to transformations of the object. For example, the symmetry of the laws of the theory of relativity is determined by their invariance with respect to the Lorentz transformations.

The determination of the set of transformations that leave unchanged all structural relations of an object—that is, the determination of the group G of the object’s automorphisms—has become a guiding principle of contemporary mathematics and physics. This principle permits the internal structure of the object as a whole and of its parts to be studied more deeply.Since such an object can be represented by the elements of some space P that possesses a corresponding characteristic structure, transformations of the object induce transformations of P.

Thus, the representation of a group G in a group of transformations of P (or simply in P) is obtained, and the investigation of the symmetry of the object reduces to an investigation of the action of G on P and to a search for the invariants of this action. In like manner, the symmetry of the physical laws that control an object under investigation and that usually are described by the equations satisfied by the elements of P is determined by the action of G on such equations.

Figures possessing translational symmetry; the upper figure also has an infinite set of vertical twofold axes of symmetry, that is, reflection planesFor example, if some equation is linear in a linear space P and remains invariant under the transformations of some group G, then to each element g of G there corresponds a linear transformation T g in the linear space R of the solutions of the equation. The correspondence g → T g is known as a linear representation of G. Knowledge of all such representations of G permits the establishment of various properties of the solutions and in many cases (on the basis of symmetry considerations) is of assistance in finding the solutions themselves. This fact, in particular, explains the need of mathematics and physics for a well developed theory of linear representations of groups. In mathematics and logic, the property of a binary (two-place, two-term) relation that indicates that the relation holds for any pair of objects regardless of the order in which the objects occur in the pair. In other words, a relation R is said to be symmetric if, for any objects x and y in its domain of definition, xRy implies yRx.

Examples of symmetric relations include relations of the equality type—identity, equivalence, and similarity—and weak forms of such relations—for example, resemblance and proximity. These weak forms are known as tolerance relations. It follows from the definition of “symmetry” given above that the complements of the relations above are also symmetric; an example is the inequality relation.The relation R is said to be antisymmetric if ⌉ yRx (the negation of yRx) follows from xRy when x ≠ y—that is, if x = y invariably follows from xRy and yRx. Examples of antisymmetric relations are the relations of order (with respect to magnitude or some other ordering criterion) between numbers or other objects and the relation of inclusion between sets.With respect to logical and logico-mathematical operations, the property of symmetry is called commutativity, or permuta-bility. For example, the results of the addition and multiplication of numbers, the union and intersection of sets, and the disjunction and conjunction of propositions ( see ALGEBRA OF LOGIC) are independent of the order of the terms, factors, and so on. The concepts of symmetry and commutativity naturally extend to the case of an arbitrary number of objects.Symmetry.